Research
My research lies at the intersection of optimization and machine learning. My work tends to focus on distributed and federated learning. I am particularly interested in reconciling optimization theory with practical machine learning. Much of my research does this by leveraging tools from high-dimensional statistics. Some general research thrusts are described in more detail below.
Practical Methods for Federated Learning
Federated learning is a distributed machine learning paradigm for learning models without directly sharing data. Image from Google's federated learning comic.
In federated learning, machine learning models are trained on-device across a cohort of distributed clients, avoiding unwanted and unnecessary data aggregation. This style of learning brings with it a host of optimization challenges, including heterogeneity of clients, and the need for communication-efficiency. We develop practical methods for federated learning, that result in better on-device models with much less total communication. We focus on methods that succeed in realistic, empirical settings.
Selected Work:
- Adaptive Federated Optimization
S. Reddi, Z. Charles, M. Zaheer, Z. Garrett, K. Rush, J. Konečný, S. Kumar, H. B. McMahan. ICLR 2021. - Advances and Open Problems in Federated Learning
P. Kairouz, H. B. McMahan, et al. (including Z. Charles).
Understanding Optimization in Federated Learning and Meta-Learning
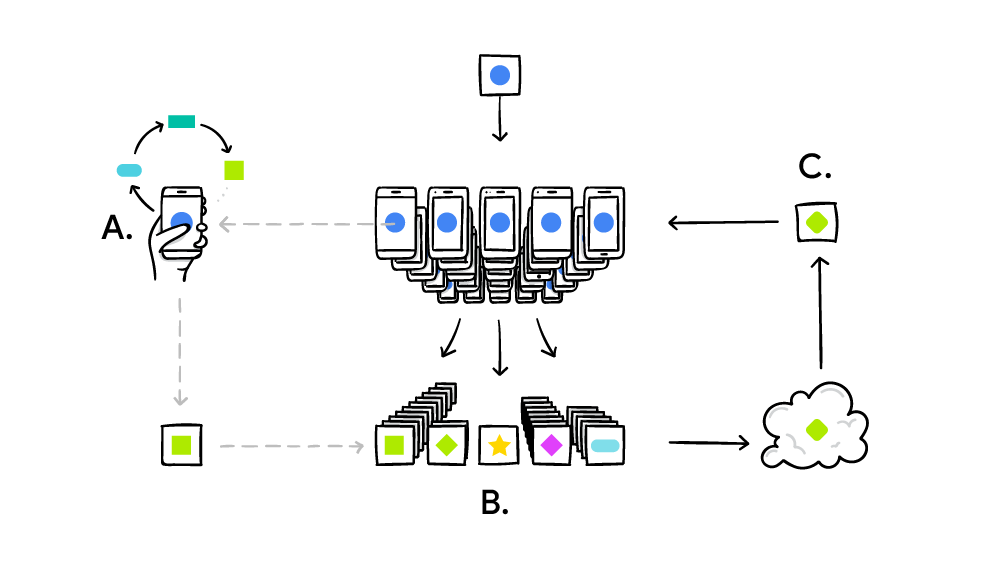
Clients perform local updates on their data (A) and their outputs are aggregated to form a server update (B). The updated server model is sent to client devices (C) and the process is repeated. Image from Google AI's blog post on federated learning.
Many optimization methods for federated learning and model agnostic meta-learning use local client updates to ensure communication-efficiency. While empirically valuable, these so-called local update methods are challenging to analyze theoretically. This makes understanding and comparing various local update methods difficult. We develop a framework to view these methods as centralized optimization methods on surrogate loss functions, allowing us to leverage existing optimization theory to compare them and understand their impact in practical scenarios.
Selected Work:
- Convergence and Accuracy Trade-Offs in Federated Learning and Meta-Learning
Z. Charles and J. Konečný. AISTATS 2021. - On the Outsized Importance of Learning Rates in Local Update Methods
Z. Charles and J. Konečný.
Robustness in Machine Learning
Popular optimization methods for machine learning, especially distributed and federated learning, can introduce vulnerabilities to adversaries, or reduce the performance of the learned model on data that has undergone minor perturbations. We analyze various types of robustness, including Byzantine robustness and adversarial robustness, in order to understand the impact of existing remedies and develop novel ones.
Selected Work:
- DETOX: A Redundancy-based Framework for Faster and More Robust Gradient Aggregation
S. Rajput, H. Wang, Z. Charles, D. Papailiopoulos. NeurIPS 2019. - Does Data Augmentation Lead to Positive Margin?
S. Rajput, Z. Feng, Z. Charles, P. Loh, D. Papailiopoulos. ICML, 2019.
Communication-Efficient Learning
In distributed systems, we often want to minimize the total amount of communication required to learn an accurate model. Communication-efficiency can manifest in different ways, including the total size of updates from clients, or from the additional communication overhead required to ensure that learning occurs even in the presence of system bottlenecks and failures. In this thrust, we develop methods that help reduce communication costs for distributed machine learning systems.